티스토리 뷰
무방향 (양수) 가중치 그래프 G =(V, E)
각 edge (u, v) ∈E에 대해서 가중치 : W(u, v)
문제 : edge들의 부분집합 T ∈ E를 찾아라
1. T에 속한 edge들에 의해 모든 정점들이 서로 연결된다
2. 가중치의 합 ∑ w(u, v) 이 최소가 되도록 한다
(u, v)∈ T
3. 입력 : n개의 도시 도시와 도시를 연결하는 도로비용
문제 : 최소의 비용으로 모든 도시들이 연결되게 한다
어떤 부분집합 A에 대해 A ∪{(u, v)} 도 역시 MST의 부분집합일 경우 edge (u, v)는 A에 대해서 안전한다
generic -mst (G, W)
A <- 공집합
while A does not form a spannig tree do
do find an safe edge(u, v) for A
A <- A ∪{(u, v)}
return A
그래프의 정점들을 두개의 집합 S 와 V-S로 분할한 것 : cut
1. edge(u,v)에 대해서 u ∈ S 이고 v ∈V-S일때 edge(u,v)는 cross한다
2.edge들의 부분집합 A에 속한 어떤 edge이고 (S,V-S)를 cross하지않으면 컷 (S,V-S)는 A를 존중한다. respect
크루스칼
1. edge들을 가중치의 오름차순으로 정렬
2. edge들을 그 순서대로 하나씩 선택한다
이미 선택된 edge들과 cycle이 형성되면 선택하지않는다
3. n-1개 edge선택되면 종료
MST - Kruskal (G,W)
A <-공집합
for each vertex v
do MAKE-SET(v) //초기화
sort the edges of E by nondecreasing order by weight w //w 순으로 오름차순 정렬
for each edge (u,v) in nondecreasing order
do FIND-SET(u) != FIND-SET(v) //FIND-SET(v): v가 속한 집합을 찾아라
then A <- A 합집합 {(u,v)}
UNION(u,v) // u와 v가 속한 두 집합을 하나로 합친다
return A
union find
- 두 노드가 같은 그래프에 속하는지 판별하는 알고리즘
- 서로소 집합, 상호 베타적 집합(Disjoint-Set)으로도 불린다.
- 노드를 합치는 Union연산과 노드의 루트 노드를 찾는 Find연산으로 이루어진다.
- 트리 구조
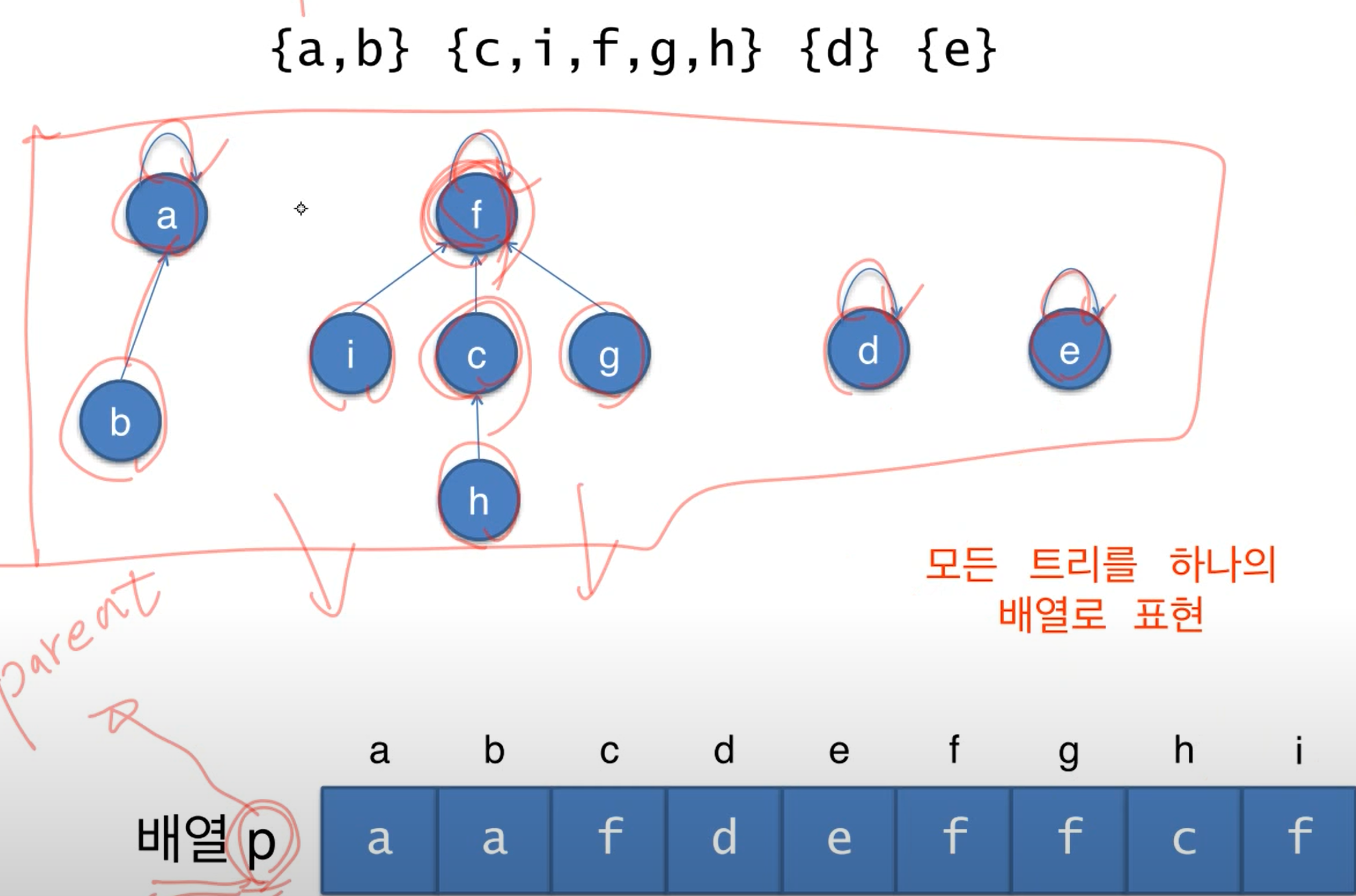
FIND-SET (x) //x가속합 집합의 루트,부모 찾기
if x!= p[x]
then p[x] <- FIND-SET(p[x])
return p[x]
UNION(u,v)
x <- FIND-SET(u);
y <-FIND-SET(v);
p[x] <- y;2. 프림
